Tasks
|
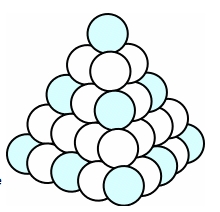
Put the four pieces together to form a pyramid. Hint: Where can you place the long pieces? |
|
A pyramid (tetrahedron) of side length 4 contains 20 balls. How many balls would be in a pyramid of side length 5? |
|
How many balls would be in a pyramid of side length 12? Is there a general way to work it out? |
|
Maths
We want to make a pyramid (tetrahedron) of side length 4. Each face is a triangle, made from a row of 4, a row of 3, a row of 2 and a row of 1. There is only one way the pieces can be stacked to make these rows.
Starting from the top, the number of balls in each layer is: 1 ball; 3 balls; 6 balls; 10 balls. These are called triangle numbers, and each triangle number is the sum of consecutive numbers: 1; 1 + 2 = 3; 1 + 2 + 3 = 6; 1 + 2 + 3 + 4 = 10. The next triangle number is 15, making a pyramid of 35 balls.
The first twelve triangle numbers are: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78.
|
History
Famous English explorer Sir Walter Raleigh wanted to know the most efficient way to store cannonballs. Should he stack them like a tetrahedral pyramid, a square pyramid, or some other way? He asked mathematician Thomas Harriot who calculated that the tetrahedral pyramid and the square pyramid were both equally efficient, with a density of 74%. But was there a better method? It took over 400 years to prove that there wasn’t a better way.
Raleigh’s second question was whether a square number of cannonballs could be made into a square pyramid. There are only two ways to do this, with 1 cannonball and with 4900 cannonballs. For a tetrahedral pyramid there are three ways to do it, with 1 cannonball, 4 cannonballs and 19600 cannonballs.
|
People
 Thomas Hales 1958 – Present Thomas Hales 1958 – Present
Thomas Hales is an American mathematician who, in 1998, proved there wasn’t a more efficient way to pack spheres than the traditional tetrahedral packing – finally settling a 400-year-old conjecture of Johannes Kepler. |
 Maryna Viazovska 1984 – Present Maryna Viazovska 1984 – Present
Maryna Viazovska is a Ukrainian mathematician who studies sphere packing. In 2014, Maryna proved the most efficient way to pack spheres in 8 dimensions and 24 dimensions. It might sound strange but this has important applications in how we transmit messages on the internet. |
|
Applications
Sphere packing has many applications, such as finding most efficient way to store items like oranges or grain.
A more surprising application to go beyond the normal 3-dimensional spheres and to consider spheres in higher dimensions. This is used to correct any misakes that might occur when transmitting messages on the internet.

|
Maths at Home
A fun question to ask at Christmas is: How many presents were given in total in the song “The 12 Days of Christmas”?

Well, each day the number of presents is a triangle number. For example, on the fourth day of Christmas there are 10 presents: four calling birds, three French hens, two turtledoves and a partridge in a pear tree.

What are the first 12 triangle numbers? Can you list them?
Add up all these triangle numbers to find the total number of presents. This is also the 12th tetrahedral number.
Are there enough presents for each day of the year?
|