Conic Sections
Tasks
|
||||||
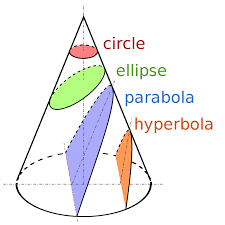
MathsAs you change the angle you will see the cross-section change. These are called conic sections. There are four types of conic section: When the cone is vertical you will see a circle. As the angle becomes steeper, the circle will change into an ellipse. When the liquid is parallel to the side of the cone, we have a parabola. This this the curve a ball makes in the air. Continue to make the angle steeper, and we will make hyperbola. This is the curve traced by a shadow on the ground throughout a day. |
||||||
HistoryConic sections were studied by the Ancient Greek mathematicians, including Euclid and Archimedes. Another Ancient Greek mathematician, called Apollonius of Perga, wrote eight books describing the different kinds of conic sections and their properties. |
||||||
People |
||||||
ApplicationsThe parabola is the curve a ball makes when thrown through the air. The shape is also used in antenna to pick up radio signals, or used in headlights to make a strong beam of light. The hyperbola is the curve traced by a shadow on the ground during a day, and is used in the design of sundials. In astronomy, gravity will cause a planet to orbit around a sun in an ellipse. On the other hand, if two objects are not in orbit, gravity will cause them to move in a parabola or hyperbola. |
||||||
Maths at HomeExplore the cross sections of different shapes with these online demonstrations from GeoGebra and Interactive However, if you want to get more hands-on, why not make the shapes yourself using play-doh. You can then (safely) slice the shapes and discover the cross sections inside. See if you can you find all the cross sections in this table. |