Tasks
|
Put one of the pictures through the slit into the mirror box. See the beautiful patterns reflected. |
|
Can you see two types of reflection? Can you find a rotation of the original image? |
|
Is there a pattern to the rotations and reflections? Do the mirrors create all possible rotations and reflections? |
|
Maths
One mirror creates a reflection, two mirrors in parallel create reflections and reflections-of-reflection. Two sets of parallel mirrors will do that in two dimensions, to create an infinite plane.
Any point reflected in a mirror is reflected with equal distance behind the mirror. This has the effect of flipping the image. A reflection of a reflection has the effect of flipping the image twice, which puts the image back to normal. One set of parallel mirrors flips the image left-to-right, and the other set reflects the image top-to-bottom.
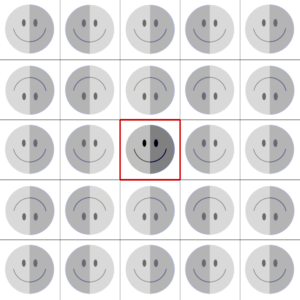 The images that are diagonal to the original have been reflected twice, but in different sets of parallel mirrors. This has the combined effect of flipping the image left-to-right and then top-to-bottom. This is equivalent to a rotation of 180˚. The images that are diagonal to the original have been reflected twice, but in different sets of parallel mirrors. This has the combined effect of flipping the image left-to-right and then top-to-bottom. This is equivalent to a rotation of 180˚.
The different rotations and reflections create a kind of checkerboard pattern. However, the two sets of parallel mirrors cannot create rotations of 90˚.
|
History
Rotations and reflections have been studied for thousands of years. A lot of decorative art uses infinite patterns of rotations and reflections, in particular you will see this in Islamic and Ancient Egyptian art.
 More recently, Dutch artist M. C. Escher was famous for incorporating mathematical ideas of symmetry into his work. More recently, Dutch artist M. C. Escher was famous for incorporating mathematical ideas of symmetry into his work.

|
People
 Evgraf Fedorov 1853 – 1919 Evgraf Fedorov 1853 – 1919
Evgraf Fedorov was a Russian scientist and mathematician who studied the structure of crystals and minerals. Wallpaper groups are all the different ways to tile the plane by rotations and reflections. Fedorov worked out that there are exactly 17 wallpaper groups. He also proved there are 230 space groups, which are like wallpaper groups but in three dimensions. |
 M. C. Escher 1898 – 1872 M. C. Escher 1898 – 1872
M. C. Escher was a Dutch artist who incorporated many mathematical ideas into his art. A lot of his work made use of tessellations, rotations and reflections. Escher also drew inspiration from Islamic art and nature. Escher would use drawings of insects and plants to tile the plane. All the different possibilities are known as wallpaper groups. |
|
Applications
Group theory is the study of symmetry. The laws of symmetry can be found throughout mathematics and physics. Rotations and reflections are an example of these laws of symmetry, and they create all the symmetries of geometric shapes and solids. Reflection groups are found in the arrangement of atoms in crystalline structures, and the patterns created by kaleidoscopes.
Infinite patterns of rotations and reflections have been used as decorative art for thousands of years. In mathematics, these are called wallpaper groups (because the patterns look like wallpaper). Mathematicians have found that there are only 17 possible wallpaper groups.
|
Maths at Home
Imagine I placed an arrow in the mirror box. Can you complete this tiling, created by all the reflections of the arrow?
 Fill in the centre square of this blank tiling with your own design. Can you complete all the reflections of your design? Fill in the centre square of this blank tiling with your own design. Can you complete all the reflections of your design?
The solution for the arrow is here.
|







