Nontransitive Dice
This is a game for two players. Roll a die each and whoever rolls the highest number wins.
Tasks
|
||||||
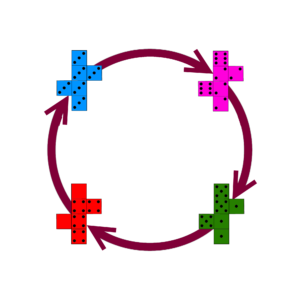
MathsThis is a set of very strange dice. If we call the four dice A, B, C and D, then A is more likely to beat B, B is more likely to beat C, C is more likely to beat D, and D is more likely to beat A! The chain of victory goes in a circle, like a game of rock-paper-scissors. Each probability in this chain is greater than 50%, so no matter which die your opponent chooses, there will always be a die that beats it. Dice like this are called nontransitive dice. It is possible to make nontransitive chains with any number of dice. |
||||||
HistoryThis strange phenomenon was first described in the 1960s by Polish mathematicians Hugo Steinhaus and Stanisław Trybuła. This set of four dice was invented in 1970 by American statistician Brad Efron, and they have been a favourite of mathematicians ever since. They are also a favourite of billionaire Warren Buffet who likes to use them to trick people. When he tried to trick his friend Bill Gates, the second billionaire was suspicious and insisted Buffet choose first. |
||||||
People |
||||||
ApplicationsNontransitive behaviour can occur in real-life situations. For example, in elections it is possible for the majority of voters to prefer candidate A over candidate B, a majority to prefer candidate B to candidate C, and the majority to prefer candidate C to candidate A. Arrow’s impossibility theorem shows that there is no voting system that is always fair. |
||||||
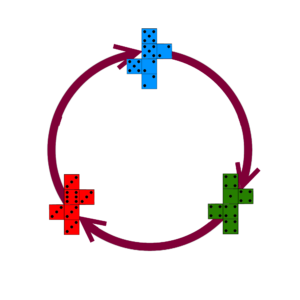
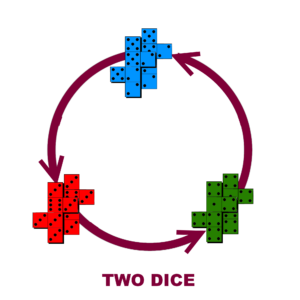
Maths at HomeWhy not make your own set of nontransitive dice! Here is a set of three dice you can make at home (here is a template to make your dice): With these dice, red beats blue, blue beats green, and green beats red. If your friend becomes suspicious, explain how the dice work and challenge your friend to one more game, one where they can choose second. But make one change – insist on rolling two of each die, so the highest total wins. Amazingly, with two dice the order of the chain flips – so the circle of victory has become a circle of defeat – and you will win again! |