Tasks
| |
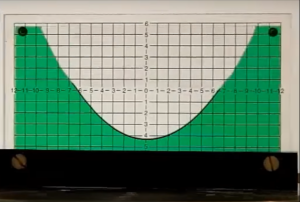
Spin the cylinder to see the liquid make a dish shape.
|
| |
What shape are the horizontal cross-sections? |
| |
What shape are the vertical cross-sections? |
|
Maths
The liquid makes a dish shape known as a circular paraboloid. The horizontal cross-sections are circles. The vertical cross sections are parabolas, the same curve a ball makes when thrown through the air.
When the cylinder spins, the liquid furthest away from the centre is moving faster, which requires a larger horizontal force to keep it moving in a circle. You may have felt this force in a fast car making a turn.
The horizontal force is provided by the liquid pushing upwards towards the surface. When the surface is steeper there is more horizontal force, so the liquid ends up creating a curve.
Specifically, the liquid is a parabolic curve. This is because the liquid that is twice as far away from the centre, needs twice the horizontal force, which makes the curve is twice as steep.
|
History
Parabolas have been studied since Ancient Greece. Greek mathematician Diocles used a parabolic mirror (a dish shaped mirror in the shape of paraboloid) to focus sunlight to create a burning mirror.
In 1663, Scottish astronomer and mathematician, James Gregory designed a telescope that used a parabolic mirror to focus light.
Famous British mathematician Isaac Newton noted that the surface of rotating liquids form a paraboloid and could be used in telescopes. But it wasn’t until 1872 that Henry Skey of New Zealand constructed the first working liquid-mirror telescope.
|
People
 Diocles c. 240BC – 180BC Diocles c. 240BC – 180BC
Diocles was a Greek mathematician. Little is known about Diocles except for his work. Diocles is thought to be the first to prove the focal property of parabolas and described using parabolic mirrors to focus sunlight to create a burning mirror. His work inspired later mathematicians who studied optics. |
 James Gregory 1638 – 1675 James Gregory 1638 – 1675
James Gregory was a Scottish astronomer and mathematician. Originally from Aberdeen, Gregory became a professor of mathematics at St Andrews, and later at the University of Edinburgh. Gregory designed a type of reflecting telescope that used a parabolic mirror to focus the light. He is also known for his work in calculus, trigonometry and infinite series. |
|
Applications
Parabolas appear in the physical world when throwing a projectile through the air, such as a ball or a jet of water.

Parabolic mirrors are widely used in astronomy to focus the light and radio signals onto one point. Parabolic mirrors are made by spinning molten glass, and then allowing it to cool as it continue to rotate, created a paraboloid.
Unfortunately, parabolic mirrors are expensive to make. A cheaper alternative, used for some large telescopes, is to use a pool of liquid mercury. The mercury is then rotated as a constant speed, creating a paraboloid. This is called a liquid mirror.

|
Maths at Home
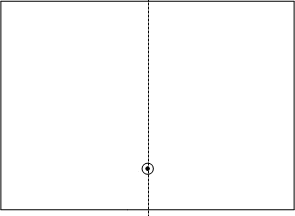
Here’s a way to make a parabola at home, using post-it notes (or similar).
- Fold the paper in half to create a vertical line of symmetry. Place a dot somewhere on this line. This is the focal point.
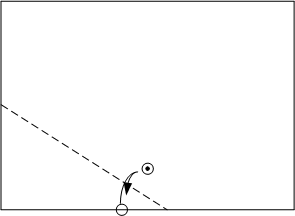
- Fold the bottom edge of the paper so that it touches the point. Make a crease and open the paper again.
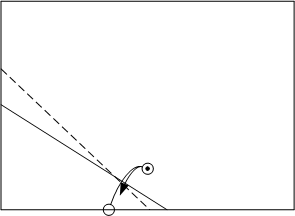
- Repeatedly fold, crease and open the paper at different spots along the edge.
- If it is difficult to see your creases, try shading the reverse of each fold, or using wax paper. The many creases will form a parabola.
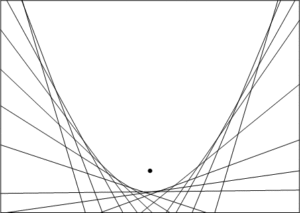
This works because each point of the parabola you make is the same distance from the focal point as it is from the bottom edge. This is one of the definitions of a parabola.
How does changing the height of the focal point affect the parabola?
|