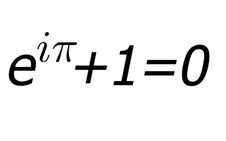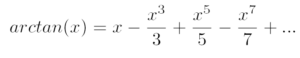Wall Maths
Euler’s Identity
Often regarded as the most beautiful equation in mathematics because it is a way to connect five of the most important mathematical constants.
Where, Pi, π, is the ratio of a circle’s circumference to its diameter.
The imaginary unit, i, is the square-root of -1 and gives us complex numbers.
Euler’s constant, e, is appears naturally in problems of growth or change.
Finally, the numbers 0 and 1 are the basis of all arithmetic.
Leonhard Euler was an 18th century Swiss mathematician, and considered one of the greatest mathematicians of all time. Euler’s formula connects the constant e with the sine and cosine of a triangle, as follows:
If we let x = π, we obtain the famous Euler’s identity.
Leibniz’s Formula
Leibniz’s formula gives us a way to calculate the mathematical constant π.
The formula uses odd numbers, and an infinite sum of fractions, to calculate π/4.
Gottfried Leibniz was a 17th century German mathematician. One of his mathematical discoveries was a formula to calculate the inverse tangent, arctan, of a number. The tangent function is the same one used in calculating sides of a triangle.
By setting x = 1, Leibniz obtained the formula for π/4.
Leibniz wasn’t the first to find the formula for arctan, as it has been previously discovered by the 17th century Scottish mathematician James Gregory, and the 14th century Indian mathematician Madhava of Sangamagrama.