Wave Tank
Tasks
|
||||||
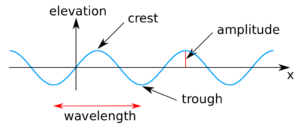
MathsOcean waves are created by wind and storms. Studying the motion of waves is important in the creation of effective coastal defences. The speed of the wave can then be calculated by dividing the wavelength, by the time taken for the wave to travel this distance, known as the period. Although the crest of the wave is travelling, underneath the surface, small volumes of water are relative stationary, and are simply moving in circles. These circular orbits become more squashed and elliptical with depth. The shape of this wave is called a trochoid. Modelling wave motion can be complicated, especially when you include factors such as turbulence. However, a sine wave can be used as a good approximation to calculate the height, shape, speed and energy of the wave. Coastal engineers use experimental data from around the world, coupled with the maths of wave motion to predict flooding. Simulations can be designed to find the most effective coastal defences for each beach. In general, the most effective coastal defences are rocks or steps as these create turbulence and dissipate wave energy. Alternatively, a slope combined with a curved wall will deflect any overspill back towards to the sea. |
||||||
HistoryCoastal defences have existed since ancient times. Two-thousand years ago, Romans built a seawall on the Mediterranean sea, creating an artificial harbour which still exist today. In the 19th century, mathematicians began describing the motion of waves mathematically. This included the shape and speed of a wave, as seen on oceans and used by coastal engineers today. Solutions to these problems can be difficult to approximate, so these equations are often simplified to give us approximations that are good enough for practical applications. |
||||||
People |
||||||
ApplicationsAs sea levels rise, coastal defences will become even more important to prevent flooding. Coastal engineers use experimental data, and the maths of wave motion, to design coastal defences. Thousands of experiments have been performed that measure the effectiveness of various types of coastal defences. This data is then used to predict the expected flooding that might occur at a given beach, allowing coastal engineers to design the most effective defences. In computer animation, the maths of wave shape and wave motion essential in creating realistic-looking oceans. |
||||||
Maths at HomeThe shape of a wave is called a trochoid, and it is the shape traced by a point on a circle as it rolls along the ground. The point tracing the wave doesn’t have to be on the edge of the circle, it can be a point inside the circle as well. This will create smaller, flatter waves. Try to make a wave shape yourself using this online Spirograph (called Inspirograph) https://nathanfriend.io/inspirograph/ What do you need to make a wave shape? How does the shape change when you use a point closer to the edge or closer to the centre? From the circle, what is the distance between peaks? What is the height of the wave? |